Aplicación del Trinomio de Bernouille y el efecto Venturi a las dinámicas de sedimentación de las espigas litorales.

Investigación y trabajo de campo:

Viajes de estudio. (1991 – 2018). Relevamientos. (2009 y 2012).

Expedición de Península de Valdés
Ing. Agr. Horacio Cerutti
Pedro Beilin
Roberto Hilson Foot

Fotografías:

Agradecimientos:
Al Doctor Roberto Kokot por sus esclarecedores comentarios.

     La tesis teórica que deseamos esbozar es que las espigas no siguen una acreción cuantificable por medio de una función lineal de primer grado. Aun suponiendo como valores constantes la incidencia del suministro de sedimentos, la energía de las olas, la dirección e intensidad de la deriva litoral, los condicionantes climáticos y mareológicos y los características batimétricas o sea manteniendo todas estas variables de acuerdo a la cláusula de “ceteris paribus” aun así, entendemos que las espigas al ir cerrando la sección areal de ingreso y egreso de las aguas a las bahías y caletas tendrían que soportar velocidades crecientes de las aguas en las partes distales de la espiga por el progresivo angostamiento del canal de acceso alterando la dinámica del fluido sobre todo en contextos macromareales, aumentando la capacidad de erosión y transporte de las aguas tendiendo a ralentizar la progradación de los sedimentos propios de la espiga y dificultando los cierres de las bahías.
    Al referirnos a la idea de que la sedimentación de la espiga no puede responder a una función lineal, entendemos que el ritmo de acreción se modifica en función del avance de la espiga y consiguientemente el ancho y profundidad del canal de acceso y egreso de las aguas o sea de la sección transversal de la boca de la bahía o caleta con modificaciones en la velocidad del agua y por lo tanto de su capacidad de erosión, transporte y sedimentación. No descartamos que empíricamente en la parte proximal las espigas puedan tender a aceleraciones en su ritmo de transporte y a aumentar el ritmo de acreción ante variaciones de los factores que en este trabajo estamos considerando como constantes o ante una rectificación de la dirección de costa que se alinea y puede aumentar el alineamiento de la fuerza hidrodinámicas incidiendo en la sedimentación y progradamiento de la espiga. Sin embargo, en algún punto de su crecimiento debemos considerar el efecto hidrodinámico variable al modificarse la velocidad del agua que ingresa y egresa a las caletas o bahía tras las espigas. Una creciente obstrucción en la sección areal de acceso debe impactar sobre las velocidades de ingreso y egreso y por lo tanto afectar la capacidad de transporte y erosión de sedimentos ralentizando paulatinamente la velocidad de progradación sedimentaria por efecto de la deriva litoral generando condiciones de creciente dificultad para los cierres sobre todo en ambientes meso y macromareales en los que aumenta la energía potencial y se fuerce el proceso al punto de no poderse lograr los cierres por simple deriva litoral necesitando eventos de tormenta que supongan un ingreso extraordinario de energía al sistema.
     Recordemos brevemente que cuando nos referimos a una función lo entendemos como una correspondencia entre los elementos de un conjunto de partida, llamado “Dominio”, en este caso será T o sea tiempo y los elementos de un conjunto de llegada, llamado “Codominio”, que para este trabajo será la longitud de la espiga, de forma tal que a cada elemento del dominio le corresponde uno, y solo uno en el codominio. Una función lineal es una función polinómica de grado 1 en la que y= ax+b, que pasa en este caso de la espiga de Páramo por el origen de coordenadas, es decir, por el punto (0,0). Son funciones rectas de la forma:

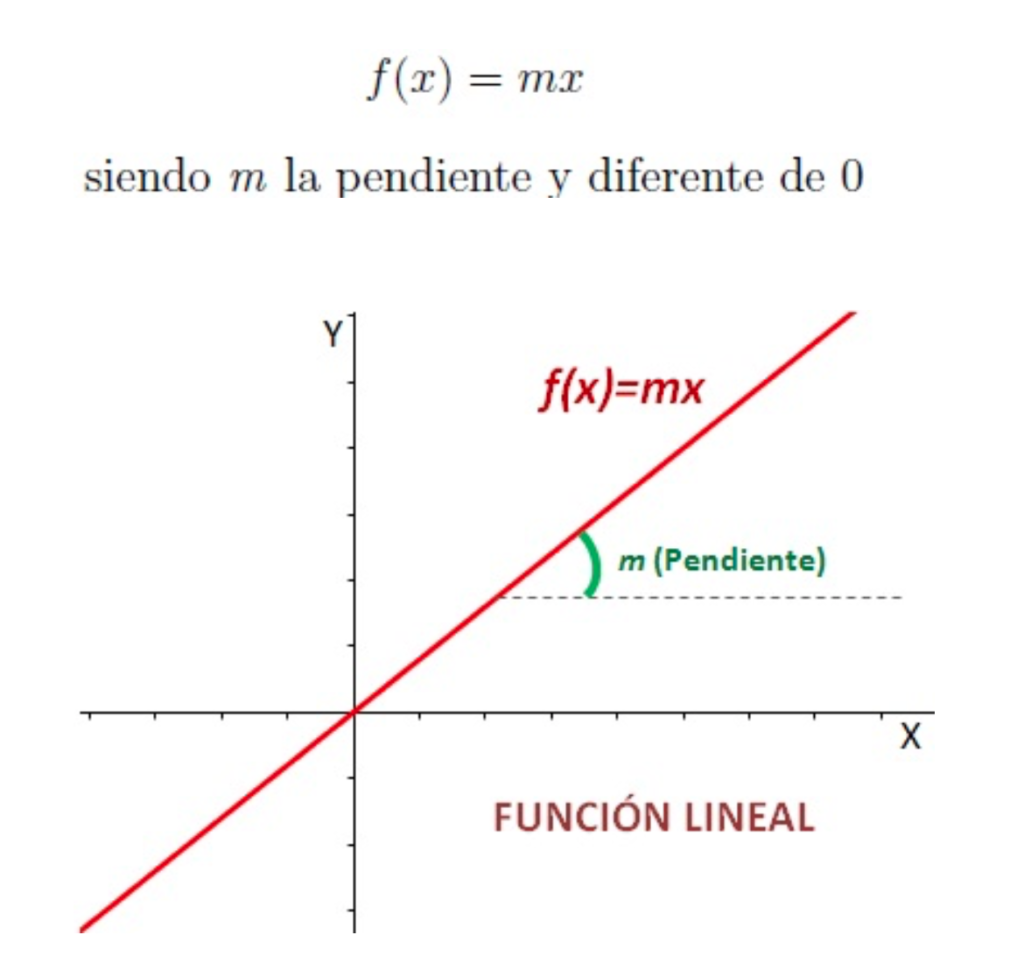
La m es la pendiente de la recta. Está pendiente indicaría el ritmo de acreción de una espiga. La pendiente es la inclinación con respecto al eje X (eje de abscisas). Si m es positiva (m > 0), entonces la función es creciente. Esto es lo que esperaríamos de una espiga en tanto las condiciones de acreción por la provisión y características de los sedimentos, la energía de las olas, la deriva litoral, las condiciones mareológicas y el clima se mantengan constantes. En cambio, si la m es negativa (m < 0), entonces la función será decreciente cosa que podría ocurrir, si por ejemplo, se disminuyera el caudal de sedimentos transportados por deriva litoral. La pendiente m significa que si aumentamos la x en una unidad la y aumenta en m unidades. Si la m es positiva, según aumente x, la y también irá aumentando (función creciente). El punto cero para nuestra hipótesis sería el proximal de la paleocosta donde por control estructural daría inicio la acreción. El punto extremo de crecimiento es el distal. Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo. Este tipo de ángulo es el que esperaríamos encontrar si las condiciones de acreción son de “ceteris paribus”.

Si m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso. Esto como decíamos podría ocurrir, por ejemplo, con una disminución en la carga sedimentaria de la deriva litoral.

     Esto significa que cruzamos la variable temporal contra una cuantificación del crecimiento sedimentario de la espiga. Si la función es lineal significará que por unidad de tiempo constante la espiga acresionará cantidades proporcionales de longitud. Si suponemos que en el eje y de las ordenadas graficamos la variable temporal y en eje x de las abscisas graficamos el tamaño de la espiga nos dará una línea de ángulo constante.
    Sin embargo, el núcleo de este trabajo desea cuestionar este supuesto al entender que no puede ser tenida como constante la hidrodinámica del sistema por el efecto de cierra del canal implícito en la acreción de la espiga en condiciones de control estructural del margen opuesto de la bahía o caleta o sea en tanto la margen opuesta no sea erosionada en proporciones similares ampliando de ese modo la sección areal.
    Con respecto al fluido podemos asumir en principio que se desplaza por suaves líneas de correntada paralelas a la velocidad y dirección predominante del fluido por tanto no crea una superficie compuesta con varias líneas de flujo y los describiremos como laminar aunque creemos que es posibles asumir la hipótesis de un flujo turbulento por los efectos de difracción en la parte distal sin alterar por ello en principio las consecuencias de la ecuación de continuidad o sea de conservación de la masa en el estado estacionario que conserva la energía mecánica. La variación en la energía del fluido estará en función de variaciones cinéticas, potenciales y/o en la presión. Este principio fue formulado por Daniel Bernoulli (1700-1782) en su libro “Hydrodynamica, sive de viribus et motibus” publicado en la actual Estrasburgo en 1738. Pertenecía a un largo linaje de matemáticos y fue hijo de Johann I Bernoulli (1667-1748) siendo profesor de Anatomía, Botánica y luego a partir de 1750 de Física en la Universidad de Basilea (Piñeiro 2017). El título del libro que hemos tenido que consultar en latín pues no hemos podido dar con traducciones en castellano o inglés hace referencia a la fuerza (viribus) y el movimiento (motibus) de los fluidos en el que representa un flujo que conserva energía un flujo volumétrico asumido en principio no turbulento en tanto el líquido presente condiciones de incompresibilidad. Leonhard Euler (1707-1783) parte del círculo de los Bernoulli y amigo de Daniel publicó el artículo “Principes gènéraux du mouvement des fluides” en el que describe al movimiento de un fluido que no se puede comprimir y que está desprovisto de viscosidad que respeta los principios de conservación de la masa momento y energía. Posteriormente Pierre-Simon Laplace (1749-1827) le agrega a las ecuaciones de Bernouille y Euler el componente adiabático o sea que la cantidad de calor es constante (Navarro Sandalinas 2017). Ese fluido es lo que se denomina fluido ideal. Sin embargo, si el flujo es no rotacional o si hay flujo turbulento la ecuación mantiene su validez (Gettys et al 1991). El otro aspecto a considerar es si medimos variaciones en la temperatura que puedan alterar la densidad y por tanto el flujo, este tema lo dejamos pendiente para futuros trabajos.
     La siguiente ecuación conocida como “ecuación de Bernoulli” (Trinomio de Bernoulli) es la que está en juego en esta hipótesis:

Para aplicar la ecuación se deben realizar los siguientes supuestos:

Viscosidad (fricción interna) = 0. Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona ‘no viscosa’ del fluido.
Caudal constante.
Flujo incompresible, donde ρ es constante.

La ecuación en su presentación inicial se aplica a lo largo de una línea de corriente o en un flujo laminar, aunque la turbulencia no altera el principio. Un ejemplo clásico de aplicación del principio se da en el flujo de agua en tuberías cuando se disminuye la sección del mismo se aumenta la velocidad del fluido que en términos hidrológicos implica un aumento en la capacidad erosiva del agua y una menor sedimentación contribuyendo a nuestro entender a una ralentización en el ritmo de sedimentación distal de una espiga. Es posible conocerla como la ecuación de la continuidad por la que la velocidad con que pasa el agua por una tubería es inversamente proporcional al área de dicha tubería, entendiendo que el caudal volumétrico tiene que mantenerse constante.
Es posible complementar el trinomio de Bernoulli con el efecto hidrodinámico conocido como efecto Venturi por el cual {\displaystyle V}un fluido en movimiento dentro de un conducto disminuye su presión cuando aumenta su velocidad al pasar por una zona de sección menor. Este efecto fue demostrado en 1797 y recibió su nombre del físico italiano Giovanni Battista Venturi (1746-1822). El efecto Venturi se explica por el Principio de Bernoulli y el de continuidad de la masa (Gettys et al 1991). El caudal disponible de un fluido lo tomamos como constante que sería el caso del ingreso del agua total de mar a la bahía, aun cuando la onda de marea sea no lineal pues la misma debe ser asumida como variable independientemente de la sección areal de ingreso y egreso a la bahía o caleta. Es posible establecer por tanto la hipótesis de que cuando las mareas están creciendo si paulatinamente la sección areal disminuye por la progradación de la espiga, necesariamente la velocidad aumenta para atravesar esta sección. Esta característica implica que ante la mayor velocidad de acceso y egreso del agua la capacidad de erosión y transporte aumenta por lo que la posibilidad de sedimentación progradante de la espiga encuentra una creciente dificultad ralentizando inevitablemente su crecimiento y dificultando los cierres de bahías y caletas.

Desde el punto de vista empírico (Palalane et al. 2014) mostraron que la variación empírica de las condiciones bajo las que progradan espigas son tan complejas que es difícil que se mantengan constantes por más de 50 años. Les ha sido muy difícil poder predecir empíricamente ritmos de sedimentación entre otras cosas por las dificultades en las recurrencias de eventos climáticos disruptivos. Esto ha llevado a los teóricos a segmentar las fases de crecimiento de forma empírica en las cuales puedan determinarse homogeneidades parciales en su desarrollo, pero basadas en meras estadísticas. Esta dificultad teórica y las limitaciones en los modelos matemáticos utilizados hasta ahora no son una objeción a nuestra hipótesis que pretende dar cuenta de variables hasta ahora no consideradas en las investigaciones. Sin duda que la ralentización de la acreción de una espiga puede provenir de varios factores como una restricción en el suministro de sedimentos o la existencia de un canal de mayor profundidad que altera drásticamente la batimetría pero esto no invalida los condicionantes físicos aplicados a la hidrodinámica sobre todo en contextos meso a macromareales en los cuales el flujo de agua tiende a ser mayor con mayor energía potencial y cinética.
Desde el punto de vista epistemológico podemos decir que la multiplicidad de método para investigar tanto las espigas en general como la espiga de Caleta Valdés nos ubica con comodidad en la consigna del epistemólogo Paul Feyerabend (1924-1994) que postuló como “todo sirve” a los fines de idear conocimientos científicos (Feyerabend 1987). Es interesante considerar que este trabajo se enmarca en el paradigma de la mecánica clásica por la escala macroscópica y gravitacional en la que se trabaja. Pero admitimos que es difícil pensar que exista una evidencia empírica cruda y objetiva por fuera de ese paradigma que ha sufrido el desplazamiento de una revolución científica a partir de la primera mitad del siglo XX. Es un ejemplo en el cual, si la hipótesis es aceptada implicaría que nuestra capacidad heurística puede incrementar la cantidad de “hechos” conocidos, incidiendo en la capacidad de formular enunciados observacionales en este caso, sobre los desarrollos geomorfológicos de las espigas. Lo extraño es que a pesar de la revolución científica generada por la relatividad y la cuántica los enunciados observacionales generados en entornos teóricos propios de la mecánica clásica pueden tener una corroboración o falsación empírica, en tanto acordemos las condiciones sobre las cuales esas observaciones y mediciones se hagan. Es un caso en que puede aplicarse la idea de que la falsación es válida como regla empírica pero insignificante como condición de la racionalidad científica (Feyerabend 1990). El lenguaje observacional que adecuamos a la mecánica clásica implica su persistente utilización por una comunidad científica (Feyerabend 1984) pero agregamos que es además un lenguaje teórico observacional adecuado a los fenómenos macroscópicos gravitacionales en tanto curiosamente pueden ser este trabajo entendido en una interacción entre contextos de descubrimiento y justificación de un paradigma ya superado por la revolución científica relativista y cuántica.

III

Es posible aplicar este modelo teórico a la Caleta Valdés que es una albufera que supera los 30 km en dirección norte-sur, ubicada al este de la península Valdés, provincia de Chubut, Argentina. Esta caleta encierra una albufera de anchura variable y de circulación restringida con el mar. Conectada con el océano por medio de un estrecho canal de marea en su extremo meridional Esta albufera se enmarca con una espiga de barrera compuesta por canto rodado, grava y arena de paralela a la línea de costa y con su extremo libre en el sur. En su interior hay un par de grupos de islas. Desde 1983 conforma una Reserva Provincial Turística de 10000 ha, creada con el objetivo de preservar la fauna local. Las conclusiones explicadas a lo largo del artículo nos permiten entender la ralentización en el ritmo de acreción distal de la espiga al punto de no lograr los reiteradamente predichos cierres de la caleta. Es el diferencial hidrodinámico de presión por el efecto Venturi el que explica que la espiga no haya obturado la caleta.

Bibliografía

Bernoulli, Daniel. 1738. Hydrodynamica, sive de viribus et motibus fluidorum. Strasburgo.

Bianchi, A. A. , Balestrini, C. F. , Isbert Perlender, H. , Osiroff, A. P. 2009. Flujos de CO₂ en el mar patagónico. VII Jornadas Nacionales de Ciencias del Mar, Bahía Blanca, Argentina.

Bujalesky, G.G. 2007. Coastal geomorphology and evolution of Tierra del Fuego, Southern Argentina. Geological Acta, Vol.5 Nº4, 337-362.

Codignotto, Jorge O. 1984. Glosario Geomorfológico Marino. Asociación Geológica Argentina. Buenos Aires.

Codignotto, Jorge O. 1997. Geomorfología y dinámica costera. El Mar Argentino y sus recursos pesqueros. 1:89-105.

D´Onofrio, Enrique, Fiore, Mónica, Saraceno, Martín, Grismeyer, Walter y Oreiro, Fernando, 2009. Comparación de constantes armónicas de mareas provenientes de modelos globales y de observaciones en el Río de la Plata y Tierra del Fuego. VII Jornadas Nacionales de Ciencias del Mar, Bahía Blanca, Argentina.

Feyerabend, Paul. 1984. Contra el método. Ediciones Orbis. Buenos Aires.

Feyerabend, Paul. 1987. Adiós a la razón. Editorial TECNOS. Madrid.

Feyerabend, Paul. 1990. Diálogo sobre el método. Ediciones Cátedra. Madrid.

Fondebrider, Jorge, 2003. Versiones de la Patagonia. Emecé Argentina. Buenos Aires.

Gettys, Edward, Keller, Frederick, Stove, Malcolm. 1991. Física clásica y Moderna. Mc Graw Hill, Madrid.

Gómez, E. A. , Borel, C. M. Martinez, D. E. , Pierini, J.O. , Raniolo, L. A. 2009. Fluctuaciones Holocenas del nivel del mar y su potencial relación con el cambio climático global. VII Jornadas Nacionales de Ciencias del Mar, Bahía Blanca, Argentina.

Grant Gross, M. & Gross, Elizabeth. 1996. Oceanography, a view of earth. Prentice Hall, New Jersey.

Grattan-Guinness, 2005. Landmark writings in Western Mathematics (1640-1940). Chapter 9 by Mikhailov, G.H. “Daniel Bernoulli”. Amsterdam.

Guilcher, Andrés.1957. Morfología litoral y submarina. Ediciones Omega. Barcelona.

Kokot, Roberto, 2010. Espigas indicadoras de proveniencia de las olas en la costa Argentina. Revista de la Asociación Geológica Argentina 67 (1): 19-26.

Kraus, Nicholas C., Asce, M. 1999. Analytical model of spit evolution at inlets. Proc. Coastal Sediments, 99.

Navarro Sandalinas, Joaquín. 2017. Euler. Del simple cálculo al análisis matemático. RBA. EDITEC. España.

Palalane, Jaime, Larson, Magnus, Hanson, Hans. 2014. Analytical model of sand spit evolution. Coastal Engineering.

Panzarini, Rodolfo N. 1984. Introducción a la oceanografía general. EUDEBA. Buenos Aires.

Piñeiro, Gustavo Ernesto. 2017. Bernoulli, el hallazgo de la ley de los grandes números. RBA. EDITEC. España.

Weiler, Nilda E. 1993. Cambios en el nivel del mar. Causas y consecuencias. Revista Ciencia Hoy, Vol. 4 Nº 23: 36-45.

Yorio, Pablo. 2001. Áreas marinas protegidas en la Argentina. Revista Ciencia Hoy. Volumen 11 Nº 64.